In the previous post, Generating the Mandelbrot set in an OpenGL ES shader, there was blockiness caused by the low precision of the fragment shader at a zoom level of just 100x. We would like to be able to scale the fractal by factors of millions to explore it properly so this is totally inadequate.

I found a blog post about emulating double precision in GLSL by using two floats to represent a value. I recommend reading it as the author gets some pretty nice results. I tried porting the code and making it work in OpenGL ES, but the my results where far from excellent.

You can see that there is an actual improvement. The emulation works!

But at a closer look the improvement is minimal.

I modified the code to account for the lower float precision but it didn’t help. In the Android Emulator it worked much better, but the emulator has a much higher float precision even with single midiump floats.

This is where I realised that even though OpenGL ES doesn’t guarantee high precision floats in the fragment shader, it does in the vertex shader!

The next post in the series shows how to use the precision of the vertex shader to greatly improve the details.

Fractals are easy to parallelize and GPUs are insanely fast at parallell tasks. Mobile devices are not intended to be used this way so we can forget about OpenCL and other GPGPU techniques and we can expect to find obscure vendor specific limitations and bugs. The final app can be found in Google Play, GPU Mandelbrot.

My long term goal is to generate entire interactive worlds on the GPU, but we have to start with something simpler. The Mandelbrot set is defined to be the set of complex numbers c, for which the formula z = z^2 + c will go towards zero when run over and over again.

All the work here will be done by the fragment shader. The rest of the app will be as simple as possible. We draw a screen filling quad and color it with our shader. How to set this up in a minimal way will be covered in a future post.

The Vertex Shader

uniform vec2 offset;
uniform vec2 scale;
attribute vec3 position;
varying vec2 c;

void main() {
    c = scale*position.xy + offset;
    gl_Position = vec4(position, 1.);
}

Very simple. The fractal coordinates are passed on to the fragment shader as the variable c and the vertex position is just converted to the 4-component representation that OpenGL requiers. No need for any matrices or other transforms. The offset and scale uniforms will allow us to pan and zoom the fractal. That’s all for the vertex shader.

The Fragment Shader

Here we immediately get reminded that we’re coding for a mobile device and not a desktop with a full fledged discreet GPU. The shader won’t compile unless it starts with the following line:

precision mediump float;

That is a precision qualifier. OpenGL ES 2 doesn’t guarantee support for full single float precision in fragment shaders. No big deal. We set the precision of floats to mediump and forget about it. On most devices mediump means 16-bit. One of those bits is used for the sign and another 5 for the exponent, which leaves 10 bits of precision for the mentissa, the actual decimals of the float. A float usually has the form (-1)^sign*1.mentissa*2^exponent.
Querying OpenGL with the following code

int range[2], precision;
GLES20.glGetShaderPrecisionFormat(GL_FRAGMENT_SHADER, GL_MEDIUM_FLOAT, range, &precision);

tells me that my device has a mediump float precision of 10.
The full fragment shader:

precision mediump float;

// The fractal coordinate in the complex plane
// Passed down from the vertex shader
varying vec2 c;

// The function that defines the Mandelbrot set
float iteration(float z) {
    return z*z + c;
}

void main() {
    float z = 0.; // The decimal point makes the zero a float
    int i;
    int MAX_ITER = 40; // How many iterations to do
    float ESCAPE_RADIUS = 16;
    for(i = 0; i < MAX_ITER; i++) {
        // If z gets outside of the escape radius
        // we know it's not part of the set
        if(z > ESCAPE_RADIUS) break;

        // Do the math
        z = iteration(z);
    }

    // If we do all the iterations and still remain inside
    // the escape radius, we say that the point belongs
    // to the set and color it 0.
    //
    // If the point escapes we color it with a gradient
    // depending on how many iterations it took it to
    // escape.
    float speed;
    if(i == MAX_ITER)
        speed = 0.;
    else
        speed = float(i)/float(MAX_ITER);

    // speed 0 -> blue
    // slower speed -> more yellow
    gl_FragColor = vec4(speed, speed, 0.5, 1.);
}

That’s all we need in the shader for a zoomable fractal viewer.

Some devices might fail to compile this fragment shader because of the dynamic for loop in it. They need to be able to unwrap loops and we have to use constants for the start and end points of the loop. How to get around this is left for a future post, but for now a workaround is to write the for loop like this:

int i;
float ESCAPE_RADIUS = 16;
for(int j = 0; j < 40; j++) {
    if(z > ESCAPE_RADIUS) break;
    z = iteration(z);
    i++;
}

It doesn’t look like a big difference but it will be as the shader gets more complicated in future posts.

Precision

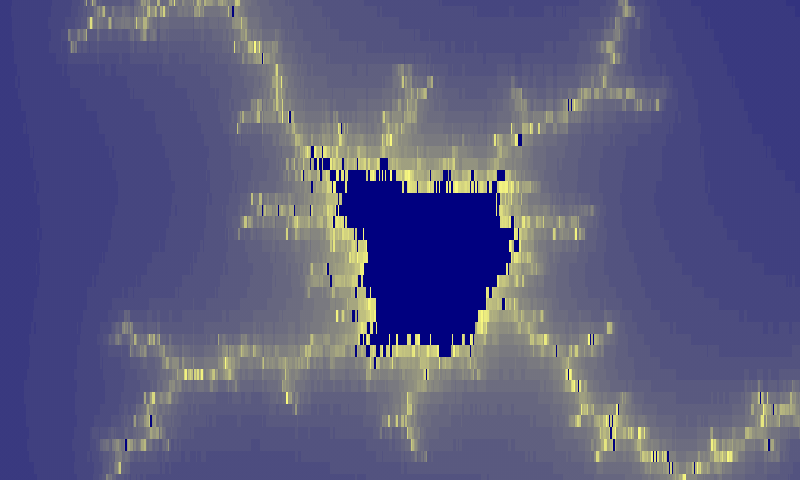
Let’s see how far we can zoom!

That’s at 100x zoom level, a scale of just 0.01. Not even remotely as good as I had hoped! The floats in our fragment shader just don’t have enough precision. That mediump at the start of the shader turns out to be a problem.

The next post in the series will be about emulating double precision in OpenGL ES shaders.