Can we start with a completely empty source file, compile it to a NES ROM and run it in an emulator? Let’s try!
Create an empty plain text file game.s and save it in a folder. It now needs to be compiled with ca65 and linked with ld65. Let’s see what happens.
If you don’t know what ca65 and ld65 are, check out Part 0: Tools needed.
Start with compiling the source file into an object file.
ca65 game.s
No error and a 251 byte game.o was created. Good so far! Now link the object file.
ld65 game.o
ld65: Error: Memory configuration missing
So, the cc65 tools can build binaries for a bunch of different 6502 based systems with different memory layouts, the NES being just one of them.
Usually you’d now need to write a detailed memory map configuration file. Luckily we don’t have to do any of that, since there is already one for the NES bundled with the compiler.
I’ll go into more technical details later on, for now let’s postpone learning about the memory layout and just get this thing working.
To use the bundled config file just specify nes as the system type. And let’s also name our output file.
ld65 -t nes game.o -o game.nes
ld65: Warning: (...)/nes.cfg(63): Segment `HEADER' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `STARTUP' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `VECTORS' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `CHARS' does not exist
A few warnings, but no errors, and a 40976 byte game.nes containing all zeroes was created.
Let’s try running it in the emualtor
fceux.exe game.nes
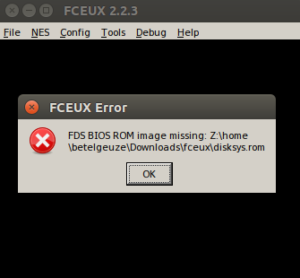
Alright, so we’re missing something. Not surprising since the ROM contains all zeroes.
ROMs need to start with the NES header. And the NES header starts with 4 specific bytes, the ASCII characters NES and the hexadecimal value 1A.
Add the following to game.s
.byte "NES" .byte $1A
And try again
ca65 game.s
ld65 -t nes game.o -o game.nes
ld65: Warning: (...)/nes.cfg(63): Segment `HEADER' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `STARTUP' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `VECTORS' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `CHARS' does not exist
fceux.exe game.nes

Same warnings and same error.
Something is wrong. Examining game.nes in a hex editor we see this:
00000000 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ................
00000010 4E 45 53 1A 00 00 00 00 00 00 00 00 00 00 00 00 NES.............
That’s strange! Our header is in there, but not at the start of the file. Instead it somehow ended up at offset $10, after 16 bytes of zeroes.
To investigate I opened up nes.cfg, the NES memory map configuration that came with cc65 and found this.
# INES Cartridge Header
HEADER: file = %O, start = $0000, size = $0010, fill = yes;
So the first 16 bytes are reserved for the header, and to use them we have to put our assembly into the HEADER segment. Should have known not to ignore those warnings.
Segments are parts of the code and data that end up in different specific areas of RAM and ROM. In the source file they are specified as .segment "SEGMEMT_NAME".
This is our new game.s that specifies that our 4 bytes go into the HEADER segment.
.segment "HEADER"
.byte "NES"
.byte $1A
Try this again now.
ca65 game.s
ld65 -t nes game.o -o game.nes
ld65: Warning: (...)/nes.cfg(63): Segment `STARTUP' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `VECTORS' does not exist
ld65: Warning: (...)/nes.cfg(63): Segment `CHARS' does not exist
Ooh! One less warning this time.
And this is what game.nes looks like in the hex editor.
00000000 4E 45 53 1A 00 00 00 00 00 00 00 00 00 00 00 00 NES.............
00000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ................
Nice, the header is in the right place. The rest of the file is all zeroes.
Let’s run it in the emulator
fceux.exe game.nes
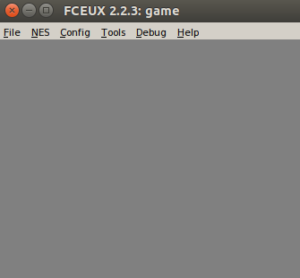
It works!
I realise this is a post about a making a ROM that doesn’t even contain any code and just draws a gray background.
It’s not useless though. This is now a ready template to fill with code and we know how to compile it.
Finally let’s just add those missing segments to get rid of the remaining warnings.
This is what game.s looks like in the end
.segment "HEADER"
.byte "NES"
.byte $1A
.segment "STARTUP"
.segment "VECTORS"
.segment "CHARS"
In the next part we’ll actually be putting something on the screen and we’ll have to talk about the different segments.